ASVAB Math Test Prep
If you are serious about getting a great score on your ASVAB Math test, try out our recommended ASVAB Math Prep Course!
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
There are 5 blue marbles, 4 red marbles, and 3 yellow marbles in a box. If Jim randomly selects a marble from the box, what is the probability of selecting a red or yellow marble?
$\dfrac{1}{4}$ | |
$\dfrac{1}{3}$ | |
$\dfrac{7}{12}$ | |
$\dfrac{3}{4}$ |
Question 1 Explanation:
The correct answer is (C). A probability is the likelihood of a successful event occurring divided by the total number of events possible. In this case, a successful event is selecting either a red or a yellow marble and the total number of events possible is the total number of marbles. Combine the number of red and yellow marbles: 4 + 3 = 7, and divide this by the total number of marbles: 5 + 4 + 3 = 12. The probability is $\frac{7}{12}$.
Question 2 |
If Kayla left a \$10.47 tip on a breakfast that cost \$87.25, what percentage was the tip?
8.3% | |
12% | |
13% | |
14% |
Question 2 Explanation:
The correct answer is (B). If you want to know what percent A is of B, you divide A by B, then take that number and move the decimal place two spaces to the right:
10.47 ÷ 87.25 = 0.12
Move the decimal two spaces to the right to find the percentage:
= 12%
10.47 ÷ 87.25 = 0.12
Move the decimal two spaces to the right to find the percentage:
= 12%
Question 3 |
A phone company charges \$2 for the first five minutes of a phone call and 30 cents per minute thereafter. If Malik makes a phone call that lasts 25 minutes, what will be the total cost of the phone call?
$8.00 | |
$8.50 | |
$9.00 | |
$9.50 |
Question 3 Explanation:
The correct answer is (A). The total cost of the phone call can be represented by the equation: TC = \$2.00 + \$0.3x, where x is the duration of the call after the first five minutes. In this case, x = 20. Substitute the known values into the equation and solve for the total cost:
TC = \$2.00 + $0.3 * 20
TC = \$2.00 + $6.00
TC= \$8.00
TC = \$2.00 + $0.3 * 20
TC = \$2.00 + $6.00
TC= \$8.00
Question 4 |
If 10 inches on a map represents an actual distance of 100 feet, then what actual distance does 25 inches on the map represent?
25 feet | |
100 feet | |
150 feet | |
250 feet |
Question 4 Explanation:
The correct answer is (D). First calculate the number of feet that 1 inch represents:
100 ft ÷ 10 in = 10 ft/in
Then multiply this by the total number of inches:
25 in × 10 ft/in = 250 ft
100 ft ÷ 10 in = 10 ft/in
Then multiply this by the total number of inches:
25 in × 10 ft/in = 250 ft
Question 5 |
Five years ago, Amy was three times as old as Mike. If Mike is 10 years old now, how old is Amy?
15 | |
20 | |
25 | |
30 |
Question 5 Explanation:
The correct answer is (B). Set up a table comparing the situation five years ago to the situation today to keep things organized.
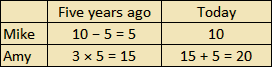
Mike is 10 years old now, so he must have been 5 years old five years ago.
Amy was 3 times as old as Mike five years ago, so Amy must have been 15 five years ago.
Add 5 years to Amy’s age five years ago to calculate her age now. Amy is 15 + 5 = 20 years old now.
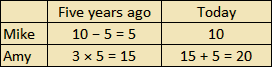
Mike is 10 years old now, so he must have been 5 years old five years ago.
Amy was 3 times as old as Mike five years ago, so Amy must have been 15 five years ago.
Add 5 years to Amy’s age five years ago to calculate her age now. Amy is 15 + 5 = 20 years old now.
Question 6 |
At a used book store, Valentina purchased three books for \$2.65 each. If she paid with a \$20 bill, how much change did she receive?
$12.05 | |
$13.15 | |
$13.85 | |
$17.35 |
Question 6 Explanation:
The correct answer is (A). Three books at \$2.65 would equal a total of \$7.95. The change would equal \$20 − \$7.95 = \$12.05.
Question 7 |
Mia earns \$8.10 per hour and worked 40 hours. Charlotte earns \$10.80 per hour. How many hours would Charlotte need to work to equal Mia’s earnings over 40 hours?
25 | |
27 | |
28 | |
30 |
Question 7 Explanation:
The correct answer is (D). Begin by calculating Mia’s total earnings after 40 hours:
40 hours × \$8.10 per hour = \$324
Next, divide this total by Charlotte’s hourly rate to find the number of hours Charlotte would need to work:
\$324 ÷ \$10.80 per hour = 30 hours
40 hours × \$8.10 per hour = \$324
Next, divide this total by Charlotte’s hourly rate to find the number of hours Charlotte would need to work:
\$324 ÷ \$10.80 per hour = 30 hours
Question 8 |
Aisha wants to paint the walls of a room. She knows that each can of paint contains one gallon. A half gallon will completely cover a 55 square feet of wall. Each of the four walls of the room is 10 feet high. Two of the walls are 10 feet wide and two of the walls are 15 feet wide. How many 1-gallon buckets of paint does Aisha need to buy in order to fully paint the room?
4 | |
5 | |
9 | |
10 |
Question 8 Explanation:
The correct answer is (B). The total number of buckets necessary will be the total area of the walls divided by the total area covered by each bucket. First, calculate the area of the walls Aisha wants to paint. Two of the walls are 10 × 10 and two of the walls are 10 × 15:
2 (10 × 10) = 200 sq. ft.
2 (10 × 15) = 300 sq. ft.
So the total square footage of the walls is 500.
If a half gallon of paint will cover 55 square feet, then each gallon will cover 2 × 55 = 110 square feet. Four gallons can only cover 440 square feet. Five gallons will cover 550 square feet, which will be enough for the entire area of the walls.
2 (10 × 10) = 200 sq. ft.
2 (10 × 15) = 300 sq. ft.
So the total square footage of the walls is 500.
If a half gallon of paint will cover 55 square feet, then each gallon will cover 2 × 55 = 110 square feet. Four gallons can only cover 440 square feet. Five gallons will cover 550 square feet, which will be enough for the entire area of the walls.
Question 9 |
There are 4 red marbles and 8 green marbles in a box. If Emma randomly selects a marble from the box, what is the probability of her selecting a red marble?
$\dfrac{1}{3}$ | |
$\dfrac{1}{2}$ | |
$\dfrac{2}{3}$ | |
$\dfrac{4}{5}$ |
Question 9 Explanation:
The correct answer is (A). The probability of a successful event is the ratio of the number of successful events to the total number of events. In this case, a successful event is selecting a red marble from the box. The total number of events is the total number of marbles in the box:
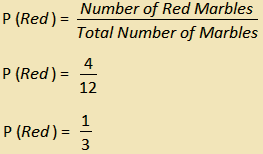
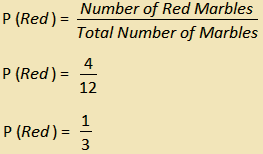
Question 10 |
Oscar purchased a new hat that was on sale for \$5.06. The original price was \$9.20. What percentage discount was the sale price?
4.5% | |
41.4% | |
45% | |
55% |
Question 10 Explanation:
The correct answer is (C). The percentage discount is the reduction in price divided by the original price. The difference between original price and sale price is:
\$9.20 − \$5.06 = \$4.14
The percentage discount is this difference divided by the original price:
\$4.14 ÷ \$9.20 = 0.45
Convert the decimal to a percentage by multiplying by 100%:
0.45 × 100% = 45%
\$9.20 − \$5.06 = \$4.14
The percentage discount is this difference divided by the original price:
\$4.14 ÷ \$9.20 = 0.45
Convert the decimal to a percentage by multiplying by 100%:
0.45 × 100% = 45%
Question 11 |
There are two pizza ovens in a restaurant. Oven #1 burns three times as many pizzas as Oven #2. If the restaurant had a total of 12 burnt pizzas on Saturday, how many pizzas did Oven #2 burn?
2 | |
3 | |
4 | |
5 |
Question 11 Explanation:
The correct answer is (B). Begin by expressing the relationship between the ovens with an equation. Use a variable to represent the number of burnt pizzas.
For every x pizzas burnt by Oven #2, Oven #1 burns 3x pizzas. It is given that 12 total pizzas are burnt, and the total number of burnt pizzas is a combination of pizzas burnt by Oven #1 and Oven #2:
x + 3x = 12
4x = 12
x = 3
The variable x represents the number of pizzas burnt by Oven #2, so answer choice (B) is correct.
For every x pizzas burnt by Oven #2, Oven #1 burns 3x pizzas. It is given that 12 total pizzas are burnt, and the total number of burnt pizzas is a combination of pizzas burnt by Oven #1 and Oven #2:
x + 3x = 12
4x = 12
x = 3
The variable x represents the number of pizzas burnt by Oven #2, so answer choice (B) is correct.
Question 12 |
Sofía is driving to Texas. She travels at 70 kilometers per hour for 2 hours, and 63 kilometers per hour for 5 hours. Over the 7 hour time period what was Sofía’s average speed?
64 km/h | |
65 km/h | |
66 km/h | |
67 km/h |
Question 12 Explanation:
The correct answer is (B). To find the average over the entire trip, use:
Average Speed = Total Distance ÷ Total Time.
Begin by calculating the total distance traveled:
Total Distance = 2(70) + 5(63)
= 140 + 315
= 455 km
Next find the total time:
Total Time = 2 hours + 5 hours
= 7 hours
Substitute these values into the average speed formula to solve:
Average Speed = 455 ÷ 7
= 65 km/h
Average Speed = Total Distance ÷ Total Time.
Begin by calculating the total distance traveled:
Total Distance = 2(70) + 5(63)
= 140 + 315
= 455 km
Next find the total time:
Total Time = 2 hours + 5 hours
= 7 hours
Substitute these values into the average speed formula to solve:
Average Speed = 455 ÷ 7
= 65 km/h
Question 13 |
Stephen signed up to bring 5 gallons of lemonade to the company picnic. He has a 5-gallon bucket which contains 3.5 gallons of lemonade. How many pints of lemonade will he need to add in order to fill the bucket?
6 | |
8 | |
10 | |
12 |
Question 13 Explanation:
The correct answer is (D). He needs 1.5 gallons. There are 4 quarts in a gallon, so he will need 6 quarts. There are 2 pints in a quart, so he needs to add 12 pints.
Question 14 |
If a car travels 360 kilometers in 5 hours, how many kilometers will it travel in 9 hours when driving at the same speed?
72 | |
288 | |
620 | |
648 |
Question 14 Explanation:
The correct answer is (D). First calculate the distance the car travels in 1 hour:
360 km ÷ 5 hours = 72 km per hour
Then multiply this number by the total number of hours traveled:
9 hours × 72 km per hour = 648 km
Notice that the final calculation yields the correct units; this helps to confirm that the calculation is correct.
360 km ÷ 5 hours = 72 km per hour
Then multiply this number by the total number of hours traveled:
9 hours × 72 km per hour = 648 km
Notice that the final calculation yields the correct units; this helps to confirm that the calculation is correct.
Question 15 |
Maya purchased a boat for \$18,340. Its value depreciated by 15% in the first year she owned it. What was her boat worth at the end of this first year?
$2,751 | |
$21,091 | |
$12,227 | |
$15,589 |
Question 15 Explanation:
The correct answer is (D). One way to solve this is to multiply 0.15 by 18,340, and then subtract this result from 18,340. An easier way is to recognize that the boat will still retain 85% of its value at the end of the first year. So you can just multiple 0.85 by 18,340:
0.85 × 18,340 = 15,589
0.85 × 18,340 = 15,589
Question 16 |
The radar system beeps once every second. How many times will it beep in 3 days?
10,800 | |
86,400 | |
129,600 | |
259,200 |
Question 16 Explanation:
The correct answer is (D). There are 60 seconds in a minute and 60 minutes in an hour. So every hour has:
60 × 60 = 3,600 seconds
There are 24 hours in a day, so each day has:
3,600 × 24 = 86,400 seconds
Multiply this by 3 to find the number of seconds in 3 days:
3 × 86,400 = 259,200 seconds
60 × 60 = 3,600 seconds
There are 24 hours in a day, so each day has:
3,600 × 24 = 86,400 seconds
Multiply this by 3 to find the number of seconds in 3 days:
3 × 86,400 = 259,200 seconds
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 16 questions to complete.
|
List |
Having trouble with the practice test?
Try our recommended ASVAB Math Prep Course! START NOW
