ASVAB Mathematics Knowledge Practice Test

ASVAB Math Test Prep

If you are serious about getting a great score on your ASVAB Math test, try out our recommended ASVAB Math Prep Course!

Try our free ASVAB Mathematics Knowledge Practice Test. This is the second of the two ASVAB math tests. There are 16 questions which must be completed within 20 minutes. The questions are designed to test your knowledge of high school math. Some of our practice problems are challenging, so take your time and be sure to double check your work. Get started now with these ASVAB Mathematics Knowledge questions.

Please wait while the activity loads.
If this activity does not load, try refreshing your browser. Also, this page requires javascript. Please visit using a browser with javascript enabled.

If loading fails, click here to try again

Congratulations - you have completed . You scored %%SCORE%% out of %%TOTAL%%. Your performance has been rated as %%RATING%%

Your answers are highlighted below.

Question 1

Simplify:

(x⁶)(x⁵)

A	2x¹¹
B	2x³⁰
C	x¹¹
D	x³⁰

Question 1 Explanation:

The correct answer is (C). Recall that the multiplication of terms sharing the same base can be simplified by adding the exponents:

x^a * x^b = x^{(a + b)}.

If this rule is forgotten, you can quickly derive it by considering the simple case of 2¹ * 2², which can be rewritten as 2 * 2 * 2, or 2³. The expression in this case, then, can be simplified as:

(x⁶) (x⁵) = x⁵⁺⁶
= x¹¹

Question 2

Solve for x:

3(x + 1) = 5(x − 2) + 7

A	−2
B	2
C	½
D	3

Question 2 Explanation:

The correct answer is (D). Begin by distributing the 3 and the 5 through their respective parentheses, then combine like terms on each side of the equal sign:
3(x + 1) = 5(x − 2) + 7
3x + 3 = 5x − 10 + 7
3x + 3 = 5x − 3

Add 3 to both sides to maintain the equality:
3x + 6 = 5x

Subtract 3x from both sides and then divide the resulting equation by 2 to solve for x as follows:
6 = 2x
3 = x

Question 3

If y = 3ab + 2b³, what is y when a = 1 and b = 2?

A	16
B	18
C	20
D	22

Question 3 Explanation:

The correct answer is (D). Substitute the given values for a and b into the equation and then evaluate to find y:

y = 3ab + 2b³
y = 3(1)(2) + 2(2³)
y = 6 + 2(8)
y = 6 + 16
y = 22

Question 4

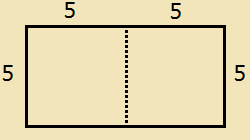
A rectangle is cut in half to create two squares that each has an area of 25. What is the perimeter of the original rectangle?

A	20
B	25
C	30
D	50

Question 4 Explanation:

The correct answer is (C). The formula to find the area of a square is: Side × Side. If each square has an area of 25, then each side of the square must be 5 (because 5 × 5 = 25). So the the dimensions of the rectangle are 5 × 10. The perimeter is the sum of all the sides, and is therefore 5 + 10 + 5 + 10 = 30.

Question 5

44 is 80% of what number?

A	51
B	53
C	55
D	57

Question 5 Explanation:

The correct answer is (C). Translate the question into an equation, using x to represent the unknown number:
44 = 0.8x

Divide both sides by the decimal:
44 ÷ 0.8 = x
x = 55

Question 6

What is the value of the expression given below?

26 − 7(3 + 5) ÷ 4 + 2

A	14
B	16.67
C	23
D	40

Question 6 Explanation:

The correct answer is (A). We can use PEMDAS to evaluate the expression. (PEMDAS is a technique for remembering the order of operations. It stands for Parentheses, Exponents, Multiplication and Division, and Addition and Subtraction) According to the rules, we must evaluate the expression in the parentheses first:

26 − 7(3 + 5) ÷ 4 + 2
= 26 − 7(8) ÷ 4 + 2

Then we perform multiplication and division in order from left to right as follows:

26 − 7(8) ÷ 4 + 2
= 26 − 56 ÷ 4 + 2
= 26 − 14 + 2

Finally, we perform addition and subtraction in order from left to right as follows:

26 − 14 + 2
= 12 + 2
= 14

Question 7

Which of the following numbers is the greatest?

$\dfrac{2}{3} \quad 0.6 \quad \dfrac{13}{22} \quad 0.08$

A	$\dfrac{2}{3}$
B	$0.6$
C	$\dfrac{13}{22}$
D	$0.08$

Question 7 Explanation:

The correct answer is (A). To determine which value is the greatest, convert the fractions to decimals and compare each value. The fraction $\frac{2}{3}$ is equivalent to 2 ÷ 3 or 0.66; the fraction $\frac{13}{22}$ evaluates to 0.59.

Question 8

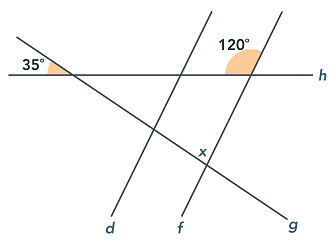
In the figure below, lines d and f are parallel and the angle measures are as given. What is the value of x?

A	55
B	75
C	85
D	90

Question 8 Explanation:

The correct answer is (C). Vertical angles are the angles opposite of each other that are created when two lines cross. Vertical angles are always equal. So, the angle vertical to the 35-degree angle also has a measure of 35 degrees. The supplement of the 120-degree angle has a measure of 60 degrees (all straight lines measure 180 degrees), so we then have a triangle with angles measuring 35, 60, and x degrees, as shown in the figure provided. Since the angles of a triangle add to 180 degrees:

35 + 60 + x = 180
x = 180 − 35 − 60
x = 85 degrees

Question 9

Simplify:

(7y² + 3xy − 9) − (2y² + 3xy − 5)

A	5y² − 4
B	9y² + 6xy − 14
C	5y² + 4
D	5y² + 6xy − 14

Question 9 Explanation:

The correct answer is (A). When subtracting polynomials the first step is to distribute the negative sign through the parentheses. This changes the sign on each term inside the parentheses:

7y² + 3xy − 9 − 2y² − 3xy + 5

Arrange like terms next to each other (optional):

7y² − 2y²+ 3xy − 3xy − 9 + 5

Combine like terms to compute the answer:

5y² − 4

Question 10

6.6 × 10⁻⁴ =

A	0.000066
B	0.00066
C	0.0066
D	0.066

Question 10 Explanation:

The correct answer is (B). Multiplying a decimal value by 10 raised to a power is equivalent to moving the decimal point to the left or right the number of times indicated by the power.

In the case of a negative exponent, the decimal is moved to the left (this is the same as dividing by 10 a number of times).

In the case of a positive exponent, the decimal is moved to the right (this is the same as multiplying by 10 a number of times).

The negative exponent here, −4, indicates that the decimal point is to be moved to the left 4 places:

6.6 × 10⁻⁴

= 0.66 × 10⁻³
= 0.066 × 10⁻²
= 0.0066 × 10⁻¹
= 0.00066 × 10⁰
= 0.00066

Question 11

What is the value of this numerical expression?

$\sqrt{6^2 + 8^2}$

A	7
B	14
C	10
D	100

Question 11 Explanation:

The correct answer is (C). According to the order of operations (PEMDAS; parentheses, exponents, multiplication, division, addition, subtraction), the exponents within the square root must be evaluated first, then the sum can be found, and finally the square root can be evaluated. The expression simplifies to:

$\sqrt{36 + 64} = \sqrt{100} = 10$

Question 12

List A consists of the numbers {2, 9, 5, 1, 13}, and list B consists of the numbers {7, 4, 12, 15, 18}.

If the two lists are combined, what is the median of the combined list?

A	5
B	7
C	8
D	9

Question 12 Explanation:

The correct answer is (C). Recall that the median of a set of data is the value located in the middle of the data set. In the case of a data set that contains an even number of numbers, the median is the average of the two middle numbers. Combine the 2 sets provided, and organize them in ascending order:

{1, 2, 4, 5, 7, 9, 12, 13, 15, 18}

Since there are an even number of items in the resulting list, the median is the average of the two middle numbers.

Median = (7 + 9) ÷ 2 = 8

Question 13

Simplify the factorial:

6! =

A	120
B	720
C	360
D	24

Question 13 Explanation:

The correct answer is (B). To solve a factorial, recall that: n! equals the product of all the whole numbers from 1 to n, so n! = 1×2×3×...×n.

6! = 1×2×3×4×5×6
6! = 720

Question 14

Solve:

(−3)³ =

A	9
B	−9
C	27
D	−27

Question 14 Explanation:

The correct answer is (D). Remember the basic rules of exponents:

n³ = n × n × n

−3³ = (−3) × (−3) × (−3)

When you multiply a negative and a negative you get a positive:
= 9 × (−3)

When you multiply a negative and a positive you get a negative:
= −27

Question 15

If 6w + 4 = 8w, then 4w =

A	1
B	2
C	4
D	8

Question 15 Explanation:

The correct answer is (D). The first step is to solve for w:
6w + 4 = 8w

Subtract 6w from both sides:
4 = 2w

Divide both sides by 2:
2 = w

Now plug in the value of w:
4w = 4(2) = 8

Question 16

Factor:

4y(3x + 2) − 2(3x + 2)

A	(4y − 2)(3x + 2)
B	(3x − 2)(4y + 2)
C	(4y + 2)(6x)
D	(3x + 2)(4y + 2)

Question 16 Explanation:

The correct answer is (A). Any part of an expression that is common to every term in the expression can be factored out. In this case, (3x + 2) is a common term and can be factored out from both parts of the expression:

4y(3x + 2) − 2(3x + 2)

= (3x + 2)[4y − 2]

Notice that distributing (3x + 2) through [4y − 2] yields the original expression; this verifies the answer.

Once you are finished, click the button below. Any items you have not completed will be marked incorrect. Get Results

There are 16 questions to complete.

←

List

→

Return

Shaded items are complete.

1	2	3	4	5
6	7	8	9	10
11	12	13	14	15
16	End

Return

Having trouble with the practice test?

Try our recommended ASVAB Math Prep Course! START NOW

Next Test: Electronics >>

Simplify:

(x6)(x5)

Solve for x:

3(x + 1) = 5(x − 2) + 7

If y = 3ab + 2b3, what is y when a = 1 and b = 2?

A rectangle is cut in half to create two squares that each has an area of 25. What is the perimeter of the original rectangle?

44 is 80% of what number?

What is the value of the expression given below?

26 − 7(3 + 5) ÷ 4 + 2

Which of the following numbers is the greatest?

In the figure below, lines d and f are parallel and the angle measures are as given. What is the value of x?

Simplify:

(7y2 + 3xy − 9) − (2y2 + 3xy − 5)

6.6 × 10−4 =

What is the value of this numerical expression?

$\sqrt{6^2 + 8^2}$

List A consists of the numbers {2, 9, 5, 1, 13}, and list B consists of the numbers {7, 4, 12, 15, 18}.

If the two lists are combined, what is the median of the combined list?

Simplify the factorial:

6! =

Solve:

(−3)3 =

If 6w + 4 = 8w, then 4w =

Factor:

4y(3x + 2) − 2(3x + 2)

(x⁶)(x⁵)

If y = 3ab + 2b³, what is y when a = 1 and b = 2?

(7y² + 3xy − 9) − (2y² + 3xy − 5)

6.6 × 10⁻⁴ =

(−3)³ =