ASVAB Math Test Prep
If you are serious about getting a great score on your ASVAB Math test, try out our recommended ASVAB Math Prep Course!
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
If $n$ is a positive integer divisible by $7$, and if $n < 70$, what is the greatest possible value of $n$?
$49$ | |
$56$ | |
$63$ | |
$69$ |
Question 1 Explanation:
The correct answer is (C). If you know one multiple of a number, you can find the other multiples by adding and subtracting that number. The number 70 is divisible by 7. The greatest multiple that is less than 70 will be 70 − 7 = 63.
Question 2 |
What is the volume of this box?
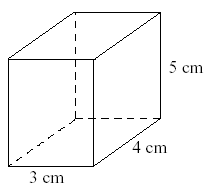
$12 \text{ cm}^3$ | |
$15 \text{ cm}^3$ | |
$20 \text{ cm}^3$ | |
$60 \text{ cm}^3$ |
Question 2 Explanation:
The correct answer is (D). The volume of a cubic rectangle is length × width × height:
$3 × 4 × 5 = 60$
$3 × 4 × 5 = 60$
Question 3 |
Blair’s average (arithmetic mean) on two physics tests is 7. What should Blair’s score be on the next test to have an overall average of 8 for all the tests?
$7$ | |
$8$ | |
$9$ | |
$10$ |
Question 3 Explanation:
The correct answer is (D). The arithmetic mean is defined as the sum of the terms divided by the number of terms.
7 = sum ÷ 2
14 = sum
Adding the next test’s score will change the average to an 8, and the total terms to 3.
8 = (14 + new score) ÷ 3
24 = 14 + new score
10 = new score
7 = sum ÷ 2
14 = sum
Adding the next test’s score will change the average to an 8, and the total terms to 3.
8 = (14 + new score) ÷ 3
24 = 14 + new score
10 = new score
Question 4 |
$(4x + 2)(x + 1) =$
$5x + 3$ | |
$4x^2 + 6x + 2$ | |
$4x+ 2x + 2$ | |
$4x^2 + 2$ |
Question 4 Explanation:
The correct answer is (B). This is a multiplying binomials problem. Multiply the first term in the first binomial by both terms in the second binomial:
$4x^2 + 4x$
Then multiply the second term in the first binomial by each term in the second binomial:
$2x + 2$
Adding them all together you get:
$4x^2 + 4x + 2x + 2$
$4x^2 + 6x + 2$
$4x^2 + 4x$
Then multiply the second term in the first binomial by each term in the second binomial:
$2x + 2$
Adding them all together you get:
$4x^2 + 4x + 2x + 2$
$4x^2 + 6x + 2$
Question 5 |
$2 − 8 ÷ (2^4 ÷ 2) =$
$-6$ | |
$-\dfrac{3}{4}$ | |
$1$ | |
$2$ |
Question 5 Explanation:
The correct answer is (C). Remember your order of operations:
$2 − 8 ÷ (16 ÷ 2) =$
$2 − 8 ÷ 8 =$
$2 − 1 =$
$1$
- Complete operations within parentheses first.
- Calculate exponents.
- Then multiply and divide in order from left to right.
- Then add and subtract in order from left to right.
$2 − 8 ÷ (16 ÷ 2) =$
$2 − 8 ÷ 8 =$
$2 − 1 =$
$1$
Question 6 |
If $3(x − 4) = 18$, what is the value of $x$?
$\dfrac{3}{2}$ | |
$\dfrac{22}{3}$ | |
$6$ | |
$10$ |
Question 6 Explanation:
The correct answer is (D). Begin by dividing both sides by $3$ to open the parenthesis:
$x − 4 = 6$
Add $4$ to both sides to find $x$:
$x = 10$
$x − 4 = 6$
Add $4$ to both sides to find $x$:
$x = 10$
Question 7 |
A scoutmaster is preparing his troop for their annual fishing expedition. He surveyed each of his scouts to find out how many fishing poles they own, and the results of the survey are shown below. What is the mode of this data set?
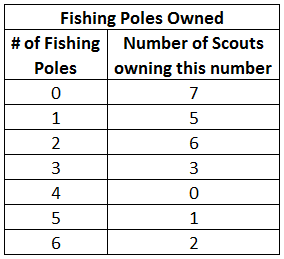
$0$ | |
$1$ | |
$2$ | |
$3$ |
Question 7 Explanation:
The correct answer is (A). The mode of the data is the number that appears the most often. In this case the largest number of scouts (7) own 0 fishing poles.
Question 8 |
A line passes through the point (−1, 2). Which of the following CANNOT be the equation of the line?
$y = 1 − x$ | |
$y = x + 1$ | |
$x = −1$ | |
$y = x + 3$ |
Question 8 Explanation:
The correct answer is (B). The slope-intercept form of a line is:
$y = mx + b$
We know the line passes through ($−1, 2$). It could have a slope, it could be vertical ($x = −1$), or it could be horizontal ($y = 2$).
Plug $x = −1$ into all four equations to see which equation is not satisfied. The only answer choice that doesn’t give us $y = 2$ is (B).
$y = mx + b$
We know the line passes through ($−1, 2$). It could have a slope, it could be vertical ($x = −1$), or it could be horizontal ($y = 2$).
Plug $x = −1$ into all four equations to see which equation is not satisfied. The only answer choice that doesn’t give us $y = 2$ is (B).
Question 9 |
If $5^{11} = 5^2 × 5^m$, what is the value of $m$?
$3$ | |
$5.5$ | |
$9$ | |
$12.5$ |
Question 9 Explanation:
The correct answer is (C). When multiplying two powers with the same base, you can always add the exponents. This means that:
$11 = 2 + m$, so $m = 9$
$11 = 2 + m$, so $m = 9$
Question 10 |
Which of these expressions is equivalent to:
$3x^3y^5 + 3x^5y^3 − (4x^5y^3 − 3x^3y^5)$
$-x^5y^3$ | |
$6x^5y^3 − x^3y^5$ | |
$7x^5y^3$ | |
$6x^3y^5 − x^5y^3$ |
Question 10 Explanation:
The correct answer is (D). The key to this problem is distributing the negative sign. When distributing a negative sign, each term has a change of sign from negative to positive or from positive to negative:
$3x^3y^5 + 3x^5y^3 − (4x^5y^3 − 3x^3y^5)$
$3x^3y^5 + 3x^5y^3 − 4x^5y^3 + 3x^3y^5$
Then simplify the expression by combining like terms:
$6x^3y^5 − x^5y^3$
$3x^3y^5 + 3x^5y^3 − (4x^5y^3 − 3x^3y^5)$
$3x^3y^5 + 3x^5y^3 − 4x^5y^3 + 3x^3y^5$
Then simplify the expression by combining like terms:
$6x^3y^5 − x^5y^3$
Question 11 |
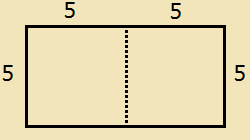
A rectangle is cut in half to create two squares that each have an area of 25. What is the perimeter of the original rectangle?
$20$ | |
$25$ | |
$30$ | |
$35$ |
Question 11 Explanation:
The correct answer is (C). The formula to find the area of a square is side x side. If each square has an area of 25, then the dimensions of the rectangle are 5 x 10. The perimeter is the sum of all the sides, and would therefore be 5 + 10 + 5 + 10 = 30.

Question 12 |
If $XY = YZ$, and angle $Y$ measures 90 degrees in the figure below, which of the following CANNOT be concluded?
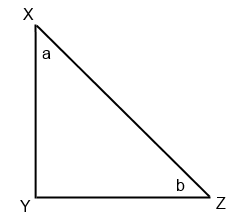
$a = b$ | |
$XZ < XY$ | |
$a + b = 90$ | |
$XZ^2 = XY^2 + YZ^2$ |
Question 12 Explanation:
The correct answer is (B). Here we are looking for the choice that is NOT true. Since the triangle is isosceles ($XY = YZ$), then $a = b = 45$. This means that $a + b = 90$. So answers (A) and (C) must be true.
For all right triangles, the Pythagorean Theorem applies, so (D) is also true.
Answer (B) is the correct answer because it is NOT true that $XZ < XY$. In a right triangle, the hypotenuse is always the longest side.
For all right triangles, the Pythagorean Theorem applies, so (D) is also true.
Answer (B) is the correct answer because it is NOT true that $XZ < XY$. In a right triangle, the hypotenuse is always the longest side.
Question 13 |
What is the value of this expression:
$\sqrt{25 + 144}$
$60$ | |
$17$ | |
$13$ | |
$11$ |
Question 13 Explanation:
The correct answer is (C). You need to add the 25 and 144 first, and then take the square root. The square root of 169 is 13 (because 13 × 13 = 169).
Question 14 |
If $(3.2 + 3.3 + 3.5)w = w$, then what is the value of $w$?
$0$ | |
$\dfrac{1}{10}$ | |
$1$ | |
$10$ |
Question 14 Explanation:
The correct answer is (A). First add up the three numbers that are in parentheses:
$10w = w$
$10w = w$ will only be true when $w = 0$.
$10w = w$
$10w = w$ will only be true when $w = 0$.
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 14 questions to complete.
|
List |
