ASVAB Math Study Guide Part 3

Algebra

This is the third part of our free ASVAB Math Study Guide. It covers algebra along with several other related topics. Read this section carefully and be sure to study the examples that are given. At the bottom of the page there is a review quiz to test your algebra skills.

Solving for x in a Basic Equation

The goal with algebra is to solve for a given variable or variables. Most often, the variable you will be solving for will be represented by x. The goal is to get x by itself on one side of the equal sign. To do this, we work in “reverse-PEMDAS” order. And, anything we do on one side of the equal sign, we must also do to the other side.

Let’s look at some examples:

Example 1:
x + 3 = 7

We are looking for the x value that when added to 3 will give us 7. Even without algebra we can see that x will need to be 4, but let’s see how we would use algebra to solve the equation. We need to get x by itself. To do so, we need to remove the 3 from the left-hand side (LHS) of the equation. We do this by subtracting 3 from both sides:

x  + 3  =  7
     −3    −3
x  + 0  =  4
x = 4, as expected.

Example 2:
2x + 3 = 7

Here we are looking for a number, x, that when first multiplied by 2 (doubled) and then added to 3 will give us 7. We could guess and check until we found a number that worked, but let’s instead use the superior approach that algebra offers. We need to get x by itself. And we need to work in “reverse-PEMDAS” order. This means we need to deal with the “add 3” before we deal with the “multiply by 2.” First subtract 3 from both sides and then divide both sides by 2:

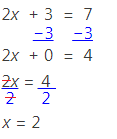
Example 3:
2x − 2 + x − 3 = 6 − 2

We now need to deal with the concept of “collecting like terms”. This simply means combining the numbers with each other and combining the x’s with each other on each side of the equation. We “collect like terms” on each side before we do anything else. Let’s first deal with the right-hand side (RHS) since it is simpler:

6 − 2 = 4, so we now have:
2x − 2 + x − 3 = 4

Let’s rewrite the equation so that the x terms and the numbers are next to each other:

2x + x − 2 − 3 = 4

On the left-hand side (LHS), we can combine the numbers. We have a −2 and a −3 which combine to give us −5. If you struggle with this, it may help to think of the equation this way:

2x + x + (−2) + (−3) = 4
We need to add −2 to −3: (−2) + (−3) = −5

2x + x − 5 = 4

Let’s now combine our x terms:

2x + x = 3x

Rewriting our equation we have:

3x − 5 = 4

We can solve this using a similar approach to Example 2:

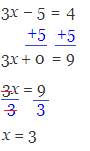
Solving for x in an Inequality

The process of solving for x in an inequality is nearly the same as it is in an equality. The difference is that when you divide (or multiply) by a negative number, the inequality sign changes direction.

Example 1:
5x + 15 ≥ 50

We begin just as we would with an equality, subtracting 15 from both sides:

5x  + 15 ≥ 50
       −15  −15
5x           ≥ 35

We then divide both sides by 5. Since we are dividing by a positive number, the inequality remains unchanged:

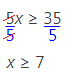
Example 2:
−3x − 12 ≥ 18

We begin just as we would with an equality, adding 12 to both sides:

−3x − 12 ≥ 18
         +12  +12
−3x          ≥ 30

Next, we divide both sides by −3. Because we are dividing by a negative number, we must flip the inequality sign:

Ratios and Equivalent Proportions

Ratios

Ratios represent the amount of one quantity in comparison to another quantity.

For example, we might say the ratio of female nurses to male nurses at a certain hospital is 5 to 3, which is written mathematically as 5:3.

What would be the ratio of female nurses to all nurses at that same hospital? For every 5 female nurses there are 3 male nurses, meaning that for every 8 (male or female) nurses, 5 of them are female. Thus, the ratio of female nurses to total nurses is 5:8.

Ratios can also be written as fractions. 5:8 can be written as $\frac{5}{8}$.

Numbers that can be written as fractions (ratios) are called Rational numbers.

Equivalent Proportions

We can use ratios to solve problems involving equivalent proportions.

Equivalent proportions are ratios that are set equal to one another. It is crucial to make sure that the numerator of the left-hand side ratio represents the same thing as the numerator of the right-hand side ratio; and, the denominators of each ratio must also represent the same thing:

$\dfrac{3 \text{ male nurses}}{5 \text{ female nurses}} = \dfrac{x \text{ male nurses}}{y \text{ female nurses}}$

$\text{ or}$

$\dfrac{5 \text{ female nurses}}{3 \text{ male nurses}} = \dfrac{y \text{ female nurses}}{x \text{ male nurses}}$

It does not matter whether we put “Male nurses” or “Female nurses” in the numerator, as long as we are consistent on the left and right sides of the equation.

Example 1:
The ratio of female nurses to male nurses at a certain hospital is 5 to 3, and there are actually 20 female nurses at the hospital. How many male nurses are there?
Let’s set up an equivalent proportion, where $x$ represents the number of male nurses at the hospital:

$\dfrac{5}{3} = \dfrac{20}{x}$

To solve this equation, we begin by “cross multiplying” and then use algebra to isolate (solve for) $x$:

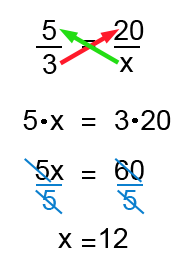
In our hospital there are 12 male nurses.

Now that you’ve read more of our lessons and tips for the Mathematics section of the ASVAB, put your skills to practice with the review quiz below. Try not to reference the above information and treat the questions like a real test.

Part 3 Review Quiz:

ASVAB Math Study Guide Part 4 >>