Polynomials
This is the fourth part of our free ASVAB Math Study Guide. This part covers polynomials, and shows two methods for multiplying polynomials. Read through this section carefully and be sure to study the examples that are given. At the bottom of the page there is a review quiz to test your knowledge of polynomials.
Polynomial Basics
Recall that when we multiply numbers raised to a power, we add their exponents:
$7^2 \cdot 7^3 = 7^{2 + 3} = 7^5$
We do the same thing when multiplying variables raised to a power:
$x^2 \cdot x^3 = x^{2 + 3} = x^5$
If the variables have coefficients, we just multiply the coefficients together and put the result as the coefficient in front of the result we get for the variable portion:
$4x^2 \cdot 6x^3 = (4 \cdot 6)x^{2 + 3} = 24x^5$
Polynomial Terms
Each “chunk” of coefficients and/or variables is called a term. Examples of terms include:
$3, \;$ $x, \;$ $2x, \;$ $3x^2, \;$ and $24x^5$
A polynomial is just the sum of one or more terms. Examples include:
$2x, \;$ $x + 3, \;$ $3x^2 + 2x, \;$ $3x^2 − 4, \;$ and $3x^2 − 2x + 1$
Like Terms of a Polynomial
We use “Like Terms” to describe a set of polynomial terms that are alike.
Constants (standalone numbers) combine with other constants; terms with specific variable and exponent combinations combine with other matching terms (regardless of whether or not the coefficients are the same).
Examples of Like Terms:
$5$ and $7$
$3x$ and $8x$
$10x^2$ and $−6x^2$
$3x^3y^5$ and $17x^3y^5$
To combine like terms, we add the coefficients together and put this new coefficient in front of the term. In the case of constants, we just add them together.
Examples of Combining Like Terms:
$5 + 7 = 12$
$3x + 8x = 11x$
$3x + 5 + 8x + 7$ $ = (3 + 8)x + (5 + 7)$ $ = 11x + 12$
$10x^2 + 3x + 5 − 6x^2 + 8x + 7$ $= (10 − 6)x^2 + (3 + 8)x + (5 + 7)$ $ = 4x^2 + 11x + 12$
$3x^3y^5 − 10x^4y^2 + 17x^3y^5 + 3x^4y^2$ $ = (3 + 17)x^3y^5 + (−10 + 3)x^4y^2$ $ = 20x^3y^5 − 7x^4y^2$
Multiplying Polynomials
When multiplying polynomials, every term must be multiplied by every other term and added together. You might think of it as the beginning of a business meeting between two companies where each person from Company A (the first polynomial) must shake hands (multiplication) with each person from Company B (the second polynomial) at the meeting, but each person does not shake hands with people from his/her own company. The result is the sum of all of the handshakes.
Example 1:
$(3)(x + 2)$
In this example, the first polynomial (using a loose definition) is simply the number $3$ and the second polynomial is $x + 2$. Company A has one representative ($3$) and Company B has two representatives ($x$ and $2$) at the meeting. $3$ must “shake hands” with both $x$ and with $2$. The result is the sum of all handshakes:
Handshake 1: $\; 3 \cdot x = 3x$
Handshake 2: $\; 3 \cdot 2 = 6$
Sum of Handshakes $= 3x + 6$
Example 2:
$(5x)(2x^2 + 4)$
In this example, the first polynomial is $5x$ and the second polynomial is $2x^2 + 4$. Company A has one representative ($5x$) and Company B has two representatives ($2x^2$ and $4$) at the meeting. $5x$ must “shake hands” with both $2x^2$ and with $4$. The result is the sum of all handshakes:
Handshake 1: $\; 5x \cdot 2x^2 = 10x^3$
Handshake 2: $\; 5x \cdot 4 = 20x$
Sum of Handshakes $= 10x^3 + 20x$
Example 3:
$(5x + 3)(2x − 4)$
Before starting, it might be helpful to rewrite the problem this way; instead of our second polynomial being “$2x$ minus $4$”, we think of it as “$2x$ plus negative $4$”:
$(5x + 3)(2x + (-4))$
In this example, the first polynomial is $5x + 3$ and the second polynomial is $2x + (-4)$. Company A has two representatives ($5x$ and $3$) and Company B has two representatives ($2x$ and $-4$) at the meeting. $5x$ and $3$ must each “shake hands” with both $2x$ and with $-4$. The result is the sum of all handshakes:
Handshake 1: $\; 5x \cdot 2x = 10x^2$
Handshake 2: $\; 5x \cdot (−4) = 5 \cdot (-4)x = −20x$
Handshake 3: $\; 3 \cdot 2x = 3 \cdot 2 \cdot x = 6x$
Handshake 4: $\; 3 \cdot (-4) = -12$
Sum of Handshakes $= 10x^2 − 20x + 6x − 12$ $ = 10x^2 − 14x − 12$ (always combine like terms)
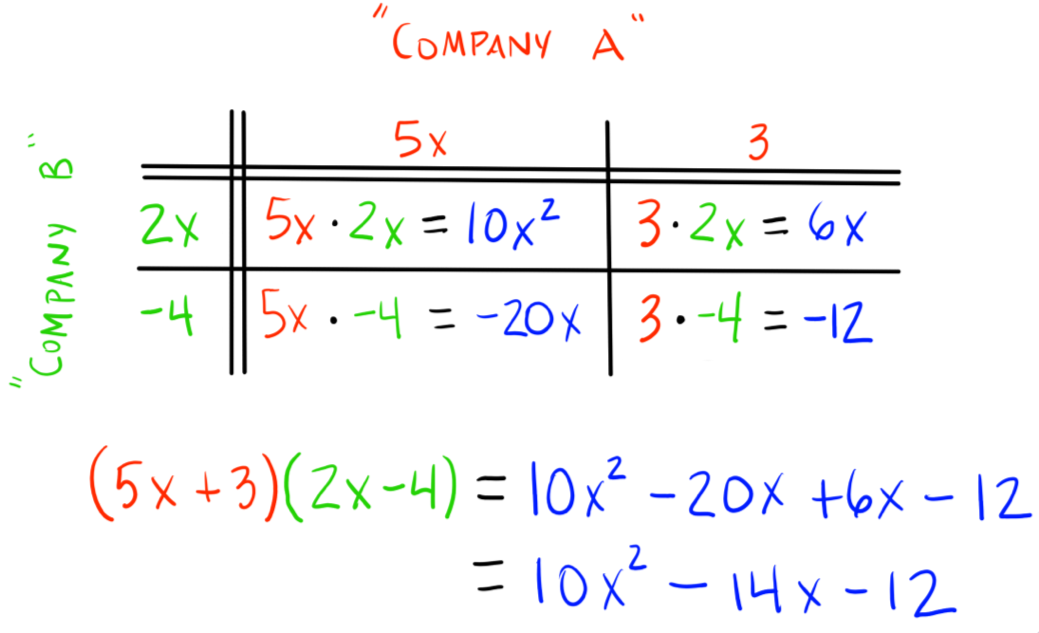
Multiplying Polynomial Using a Grid
You may find it beneficial to set up these problems in a grid. For many, it is a helpful organizational tool.
Let’s revisit Example 3 from above, but use a grid approach:
$(5x + 3)(2x – 4)$
We have 2 terms in the first polynomial (“Company A”) and 2 terms in the second polynomial (“Company B”). This means we want to set up a 2×2 grid as follows:
Now that you’ve studied another ASVAB Math lesson, put your skills to practice with the review quiz below. Try not to reference the above information and treat the questions like a real test.
Part 4 Review Quiz:
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Question 1 |
$x^7 \cdot x^2 =$
$x^{14}$ | |
$x^9$ | |
$9x$ | |
$14x$ |
Question 2 |
$9x^3 \cdot 8x^5 =$
$72x^{15}$ | |
$17x^{15}$ | |
$17x^8$ | |
$72x^8$ |
Question 3 |
$4x(6x + 2) =$
$24x + 8x$ | |
$32x$ | |
$24x^2 + 8x$ | |
$10x^2 + 6x$ |
Next, multiply $4x$ by $2$. This is simply $8x$,since $2$ was not accompanied by another variable. Thus, the simplified equation is $24x^2 + 8x$.
$x^2$ and $x$ do not count as like terms, so the equation cannot be reduced any further.
Question 4 |
$(4x + 3x)(7x − 5) =$
$7x^2 − 35x$ | |
$49x^2 − 35x$ | |
$28x^2 − 20x + 3x$ | |
$14x^2$ |
$(7x) (7x − 5)$
Then distribute the $7x$ term:
$(7x) (7x) + (7x) (-5)$
$49x^2 – 35x$
Question 5 |
$(2x^2 + 2x)(6x + 1) =$
$26x^2 + 2x$ | |
$12x^3 + 14x^2 + 2x$ | |
$12x^3 + 2x$ | |
$4x^2 + 7x$ |
Next, multiply $2x$ by $6x$ and $1$. This results in $12x^2$ and $2x$.
Combining our results, we get $12x^3 + 2x^2 + 12x^2 + 2x$.
Add like terms together to get the final answer:
$12x^3 + 14x^2 + 2x$
Question 6 |
$(2x + 3)^2 =$
$2x^2 + 3^2$ | |
$2x^2 + 9$ | |
$4x^2 + 12x + 9$ | |
$10x^2 + 6x +9$ |
Multiplying $2x$ by everything in the second set of parentheses, you get $4x^2$ and $6x$.
Multiplying $3$ by everything in the second set of parentheses, you get $6x$ and $9$.
Putting all that together, you get $4x^2 + 6x + 6x + 9$.
Combine like terms to get the final answer: $4x^2 + 12x + 9$.
Question 7 |
$2x^2(3x^2 − 8) =$
$6x^4 − 16x^2$ | |
$6x^2 − 16x^2$ | |
$6x^2 − 16x$ | |
$5x^4 − 6x^2$ |
Question 8 |
$7y^2 + 5xy − 9 − (2y^2 + 3xy − 5) =$
$5y^2 + 2xy − 4$ | |
$5y^2 + 8xy − 14$ | |
$9y^2 + 8xy − 4$ | |
$5y^2 + 2xy − 14$ |
$7y^2 + 5xy − 9 + (−2y^2) + (−3xy) + (5)$
Reorganize so like terms are next to each other:
$7y^2 − 2y^2 + 5xy − 3xy − 9 + 5$
Combine like terms:
$5y^2 + 2xy − 4$
Question 9 |
$3x^3y^5 + 3x^5y^3 − (4x^5y^3 − 3x^3y^5 + 2x^3y^3) =$
$−x^3y^5 − 2x^3y^3$ | |
$−x^3y^5 + 6x^5y^3 + 2x^3y^3$ | |
$6x^3y^5 − x^5y^3 − 2x^3y^3$ | |
$6x^3y^5 + 4x^5y^3$ |
$3x^3y^5 + 3x^5y^3 + (−4x^5y^3) + (3x^3y^5) + (−2x^3y^3)$
Reorganize so like terms are next to each other:
$3x^3y^5 + 3x^3y^5 + 3x^5y^3 − 4x^5y^3 − 2x^3y^3$
Combine like terms:
$6x^3y^5 − 1x^5y^3 − 2x^3y^3$
$6x^3y^5 − x^5y^3 − 2x^3y^3$
Question 10 |
$(2x^2 + 2x + 5)(4x^2 − 4) =$
$8x^4 + 8x^3 − 12x^2 − 28$ | |
$16x^3 + 12x^2 − 20$ | |
$8x^4 + 8x^3 + 12x^2 − 8x − 20$ | |
$16x^4 + 12x^2 − 8x − 20$ |
Start my multiplying out $2x^2$. $2x^2 \cdot 4x^2 = 8x^4$ and $2x^2 \cdot −4 = −8x^2$.
Next, multiply $2x$ by $4x^2$ and $−4$ to get $8x^3$ and $−8x$.
After that, multiply $5$ by $4x^2$ and $−4$ to get $20x^2$ and $−20$.
Putting all those answers together, we get $8x^4 − 8x^2 + 8x^3 − 8x + 20x^2 − 20$.
Combine like terms to get $8x^4 + 8x^3 + 12x^2 − 8x − 20$.
|
List |
