ASVAB Math Study Guide Part 5

Probability and Statistics

This is the fifth part of our free ASVAB Math Study Guide, covering probability and statistics. Topics include mean, median, mode, and range as well as the basics of probability. At the bottom of the page there is a 10-question review quiz to test your understanding of these probability concepts.

Mean, Median, Mode, and Range

Mean, Median, and Mode are referred to as “measures of central tendency” since they give you a feel for where the “center” or “average” value of the data typically lies.

Mean

When people say “Average” they mean “Mean”. To find the Mean, add up all the values and divide by the number of values.

Example: Find the mean of the following data values: $12, 9, 5, 10, 6, 13, 9, 8$

First find the sum of the values. $12 + 9 + 5 + 10 + 6 + 13 + 9 + 8$ $ = 72$

Next determine the number of values. There are $8$ values in our list.

$\text{Mean} = \dfrac{\text{Sum of Values}}{\text{Number of Values}}$ $ = \dfrac{72}{8} = 9$

 
Median

The “Middle” value when the list of values is arranged from smallest to largest. When there are two middle values, you find the mean of these two values to determine the Median.

Example: Find the median of the following data values: $13, 11, 2, 13, 3, 14, 7, 5$

First arrange the list from smallest to largest. $2, 3, 5, 7, 11, 13, 13, 14$

Next find the middle value. Since there are eight values in our list, there are two “middle” values, $7$ and $11$. The Median is the mean of these two values.

$\text{Median}= \dfrac{7 + 11}{2} = 9$

 
Mode

The “Most Common” (notice that “Mode” and “Most” start with the same two letters) value that occurs in a list of data.

Example: Find the mode of the following data values: $12, 9, 5, 10, 6, 13, 9, 8$

Here we simply need to determine which value occurs the most often. Since the value $9$ occurs twice in the list and all other values each only occur once, the $\text{Mode}= 9$.

 
Range

The largest value minus the smallest value.

Example: Find the range of the following data values: $13, 11, 2, 13, 3, 15, 7, 6$

The largest value is $15$. The smallest value is $2$.

$\text{Range} $ $ = \text{Largest Value} − \text{Smallest Value}$

$\text{Range} = 15 − 2 = 13$

 
Outliers

Values that are very low or high relative to the other values in a list of values. If you have many houses in a neighborhood in the \$250K–300K range and then one mansion that is valued at \$3M, we would call the value of the mansion an “outlier” in our set of data.

The methods for determining whether or not a value is truly an outlier are beyond the scope of this guide, but we wanted you to at least be familiar with the term.
 

Probability Basics

Probability refers to the likelihood of an event or combination of events occurring.

Probabilities can fall anywhere from 0 to 1. 0 means the event will never occur. 1 means the event will always occur. A probability between 0 and 1 means the event will sometimes occur; the higher the value, the greater the likelihood of the event.

Probabilities are often expressed as a percentage (%) in which case they will range from 0% to 100%.

 
Probability Formula

$\text{Probability of an event}$ $ = \dfrac{\text{Number of Successful Outcomes}}{\text{Number of Possible Outcomes}}$

You might think of “Number of Successful Outcomes” as the number of ways you can win the game and “Number of Possible Outcomes” as all the different ways the game might turn out.

Example: The names of each of the states are written on ping pong balls and put in a bag. What is the probability of drawing a state with a name that begins with the letter “O”?

The Number of Successful Outcomes is the number of states with a name that starts with “O”. It turns out there are three: Ohio, Oklahoma, and Oregon.

Number of Successful Outcomes $= 3$

The Number of Possible Outcomes is the number of states we could possibly choose. There are 50 states.

Number of Possible Outcomes $= 50$

$\text{Probability that an ‘O’ state is chosen}$

$ = \dfrac{\text{Number of Successful Outcomes}}{\text{Number of Possible Outcomes}}$

$= \dfrac{3}{50} = 0.06 = 6\%$

The likelihood of this event occurring can be described as $3 \text{ out of }50$, $3/50$, $0.06$, or $6\%$.

 
Tree Diagrams

A tree diagram is a useful way to visualize more complex probability problems.

Consider a game where you first flip a coin and then roll a die. How might we determine the probability of first flipping “heads” then rolling either a $5$ or $6$?

$\text{Probability of an event}$ $ = \dfrac{\text{Number of Successful Outcomes}}{\text{Number of
Possible Outcomes}}$

We need some way to figure out the number of successful outcomes and the number of possible outcomes. A tree diagram helps us do this.

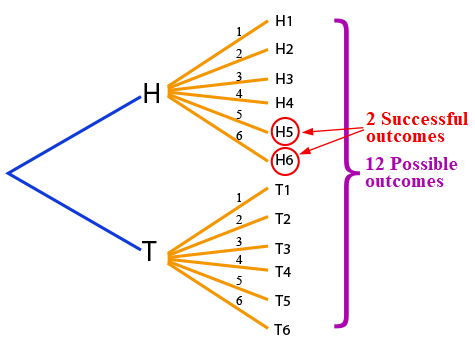
The first branch of the tree shows H (heads) and T (tails). Then for each of these branches there are 6 possible rolls of the die that could occur (1 through 6).

There are 12 possible outcomes in all: H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6 (where “T5” = flip “tails”, roll a 5)

There are only 2 successful outcomes where we first flip a “heads” then roll either a 5 or 6.

$\text{Probability of ‘heads’ then ‘5 or 6’}$

$ = \dfrac{\text{Number of Successful Outcomes}}{\text{Number of Possible Outcomes}}$

$= \dfrac{2}{12} = \dfrac{1}{6}$

Thus, the probability of flipping a “heads” then rolling either a 5 or 6 is 1/6.

 
Independent Events

The above question involving the flipping of a coin followed by the rolling of a die can also be solved using a very useful property of probability.

If two (or more) events are independent, meaning the result of one event in no way alters the result of another event, we can use the following formula:

Probability of Two Independent Events = Probability of 1st Event × Probability of 2nd Event

Let’s again consider the example above where we flip a coin and roll a die. What is the probability of first flipping “heads” then rolling either a 5 or 6?

Probability of flipping ‘heads’ $= \dfrac{\text{Number of Successful Outcomes}}{\text{Number of Possible Outcomes}}$ $= \dfrac{1}{2}$

Probability of rolling ‘5 or 6’ $= \dfrac{\text{Number of Successful Outcomes}}{\text{Number of Possible Outcomes}}$ $= \dfrac{2}{6}$

Whether we flip ‘heads’ or ‘tails’ on the coin will in no way influence the outcome of rolling the die. Thus, they are independent events, which means we can use the independent events probability formula.

Probability of Two Independent Events = Probability of 1st Event × Probability of 2nd Event

Probability of ‘heads’ then ‘5 or 6’ = Probability of ‘heads’ × Probability of ‘5 or 6’

Probability of ‘heads’ then ‘5 or 6’ $= \dfrac{1}{2} × \dfrac{2}{6}$ $= \dfrac{2}{12} = \dfrac{1}{6}$

We have a 1 in 6 chance of first flipping ‘heads’ and then rolling ‘5 or 6’ – this is the exact same result we determined with the help of the tree diagram.

Now that you’ve read more of our lessons and tips for the Mathematics section of the ASVAB, put your skills to practice with the review quiz below. Try not to reference the above information and treat the questions like a real test.

Part 5 Review Quiz:

ASVAB Math Study Guide Part 6 >>