ASVAB Math Study Guide Part 6

Geometry

This is the sixth and final part of our free ASVAB Math Study Guide. It covers geometry basics including area, volume, quadrilaterals, angles, triangles, and circles. There will always be some geometry questions on the ASVAB, so don’t skip this lesson. At the bottom of the page there is geometry review quiz to test your knowledge of these concepts.

Area of a Rectangle and Volume of a Rectangular Prism

Area of a Rectangle

$\text{Area of a Rectangle}$ $ = \text{Length} × \text{Width}$

It makes no difference which side is labeled as length and which is labeled as width as long as they are not directly across from each other.

Find the area of the rectangle shown below:

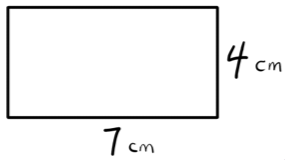
Let’s treat the 7 cm side as the Length and the 4 cm as the Width.

$\text{Area} = \text{Length} × \text{Width}$

$\text{Area} = 7 \text{ cm} × 4 \text{ cm} = 28 \text{ cm}^2$ (“centimeters squared” or “square centimeters”)

Volume of a Rectangular Prism

Rectangular Prism is the official geometric name for a 3D solid shaped like a brick.

$\text{Volume}$ $ = \text{Length} × \text{Width} × \text{Height}$

It makes no difference which sides are labeled as length, width, and height as long as they represent the three different sides of the solid.

Find the volume of the rectangular prism shown below:

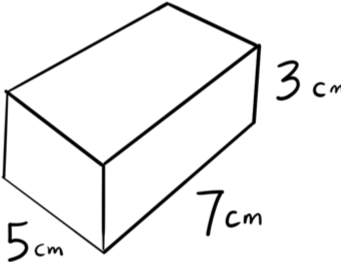
$\text{Volume}$ $ = \text{Length} × \text{Width} × \text{Height}$

$\text{Volume}$ $ = 5 \text{ cm} × 7 \text{ cm} × 3 \text{ cm} = 105 \text{ cm}^3$ (“centimeters cubed” or “cubic centimeters”)

Angles

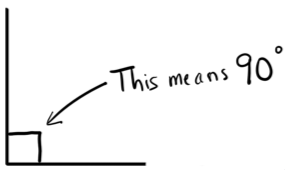
Right Angles

Just another name for a 90° angle.

So special that it gets its own symbol:

Complementary and Supplementary Angles

Complementary Angles are two adjacent (“next to each other”) angles which sum to 90°.

Supplementary Angles are two adjacent angles which sum to 180°.

“C” comes before “S” in the alphabet, and 90 comes before 180 on the number line. It is logical, then, that Complementary goes with 90° and Supplementary goes with 180°.

Complementary Angles Example:

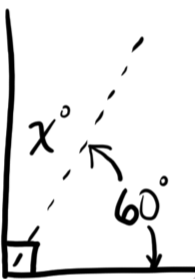
In the figure above, we can see that the two solid segments form a right angle, meaning that the angle between them is 90°. We can see that:

$60° + x° = 90°$ ($x$ is complementary to $60°$).

$x = 30$

Supplementary Angles Example:

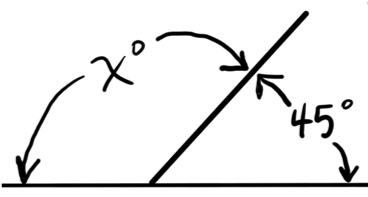
In the figure above, we can see that the two angles are both adjacent and supplementary – they are supplementary since they are formed by intersecting lines.

$45° + x° = 180°$

$x = 135$

Angles in a Triangle

The three interior angles of a triangle will always sum to 180°. This means if you know two of the interior angles, you can always find the third.

Find the missing angle in the triangle below.

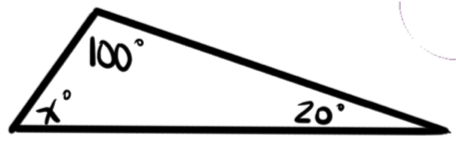
We know that the interior angles of every triangle sum to 180°:

$x° + 100° + 20° = 180°$

$x° + 120° = 180°$

$x = 60$

Triangles

Equilateral, Isosceles, and Scalene Triangles

Equilateral (“equal sides”): All three sides of the triangle will be congruent (identical); all three interior angles will be 60°.

Isosceles (“Same legs”): Two sides of the triangle will be congruent; the angles opposite the two congruent sides, called base angles, will also be congruent.

Scalene: No two sides will be the same; all three sides will have a different length and all three interior angles will be different.

Right Triangles

If any of the three interior angles in a triangle is 90°, the triangle is called a “Right Triangle” because it contains a “right” (90°) angle.

The side opposite (directly across from) the 90° is called the hypotenuse; the other two sides are called legs.

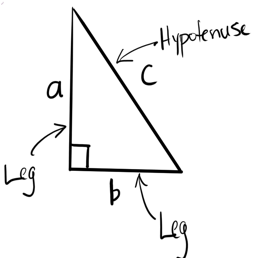
Pythagorean Theorem: Applies only to right triangles and says that $a^2 + b^2 = c^2$, where $a$ and $b$ represent the lengths of each of the legs and $c$ represents the length of the hypotenuse.

Example: Find the missing side in the triangle shown below.

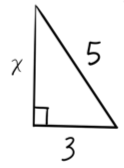
We know this is a right triangle because of the right angle symbol used in the illustration. This means we are able to use the Pythagorean Theorem.

We know that 5 is the length of the hypotenuse since it is the side opposite the right angle; the length of the hypotenuse is always “$c$” in the equation.

$a^2 + b^2 = c^2$

$3^2 + x^2 = 5^2$

$9 + x^2 = 25$

$x^2 = 25 − 9$

After subtracting $9$ from both sides:

$x^2 = 16$

$\sqrt{x^2} = \sqrt{16}$

A square root undoes a square; take the square root of both sides

$x = 4$

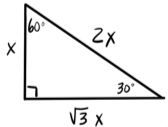
30-60-90 Triangles: A special right triangle where the interior angles are 30°, 60°, and 90°. The side lengths will always be in the same proportions as shown.

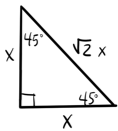
45-45-90 Triangles: Another special right triangle where the interior angles are 45°, 45°, and 90°. Because the base angles are the same, this is also an isosceles triangle. The side lengths will always be in the same proportions as shown.

Acute and Obtuse Triangles

Acute: All three of the interior angles in the triangle are less than 90°.

Obtuse: One of the three interior angles in the triangle is greater than 90°.

Area of a Triangle

The area of a triangle is always half the area of the smallest rectangle (or parallelogram) it would take to enclose it.

Typically the equation is written as $\text{Area} = \frac{1}{2} \cdot b \cdot h$, where $b$ represents the base and $h$ the height (the distance measured perpendicularly from the base to the opposite vertex).

Example: Find the area of the triangle shown.

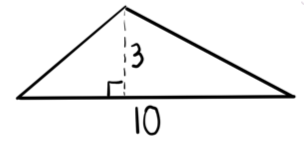
$\text{Area} = \dfrac{1}{2} \cdot b \cdot h$

$\text{Area} = \dfrac{1}{2} \cdot 10 \cdot 3 = 15 \text{ units}^2$

Quadrilaterals (“Four Sides”)

Angles in a Quadrilateral

The interior angles of a quadrilateral will always sum to 360°.

Parallelogram

A special type of quadrilateral where each pair of opposite sides is parallel. The parallel symbol is typically illustrated as a filled-in triangle(s) on each of the parallel sides.

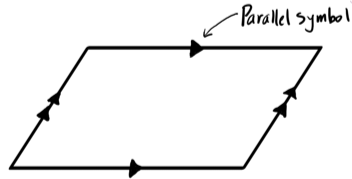
Opposite sides of a parallelogram are always congruent (same length).

Area of a Parallelogram

$\text{Area} = b \cdot h$

Example: Find the area of the figure shown.

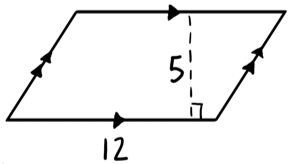
We know it is a parallelogram since each pair of opposite sides is parallel. 5 represents the height of the parallelogram since it is the perpendicular distance between opposite sides.

$\text{Area} = b \cdot h$

$\text{Area} = 12 \cdot 5 = 60 \text{ units}^2$

Rectangle

A special type of parallelogram where any (and all) of the interior angles are 90°.

Area and Perimeter of a Rectangle

$\text{Area} = b \cdot h$ (just like a parallelogram), but since rectangles are so common, the area formula is more often written:

$\text{Area} = l \cdot w$, where $l$ is the length and $w$ is the width.

Perimeter is simply the distance around an object. It can be thought of as “How far you would have to walk if you traveled along the border of the shape.”

$\text{Perimeter} = l + w + l + w$

$\text{Perimeter} = 2l + 2w$

Example: Find the area and perimeter of the rectangle shown below.

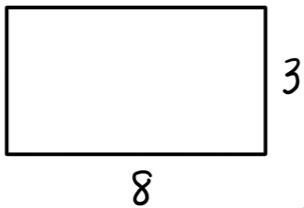
$\text{Area} = l \cdot w$

$\text{Area} = 8 \cdot 3 = 24 \text{ units}^2$

$\text{Perimeter} = l + w + l + w$

$\text{Perimeter} = 8 + 3 + 8 + 3$

$\text{Perimeter} = 2(8) + 2(3)$

$\text{Perimeter} = 16 + 6 = 22 \text{ units}$

Circles

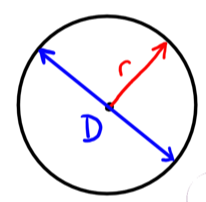
Radius and Diameter

Radius, r, is the distance from the center of a circle to a point on the circle.

Diameter, D, is the distance from one side of the circle to the other passing through the center; it is always two times the radius.

Pi (π)

Pi is the ratio of “how far around” (circumference) to “how far across” (diameter). Regardless of the size of the circle, the ratio of “how far around” to “how far across” is always the same.

$\text{Pi} = π$ $= \dfrac{\text{how far around}}{\text{how far across}}$ $= \dfrac{\text{circumference}}{\text{diameter}} ≈ 3.14$

Circumference of a Circle

As mentioned above, the circumference of a circle is the distance around the circle. It is no different than the perimeter, but circles are special enough that the perimeter of a circle gets its own name.

$\text{Circumference} = π \cdot Diameter$ $ = π \cdot D$

Since Diameter is two times the Radius, we can also use the following equation (which is the one you will most likely recognize):

$\text{Circumference} = π \cdot D = π \cdot (2r)$ $ = 2πr$

Area of a Circle

$\text{Area} = π \cdot r^2$

Example: Find the Circumference and Area of the circle below.

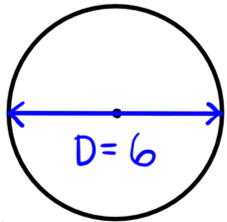
$\text{Circumference} = π \cdot D = π \cdot 6$

$\text{Circumference} = 6π \text{ units}$

“$6π$” is the exact circumference. You will often be asked for an approximate answer. To find the approximate circumference, substitute $3.14$ (typically) for $π$:

$\text{Circumference} = 6π$

$≈ 6(3.14) ≈ 18.8 \text{ units}$

 
Now let’s find the area…

$\text{Area} = π \cdot r^2$

To use the area formula we need to find the radius, $r$. $r$ is half of $D$.

$r = \dfrac{D}{2} = \dfrac{6}{2} = 3$

$\text{Area} = π \cdot r^2 = π \cdot (3)^2$ $= π \cdot 9 = 9π \text{ units}^2$

“$9π$” is the exact area. You will often be asked for an approximate answer. To find the approximate area, substitute $3.14$ (typically) for $π$:

$\text{Area} = 9π$ $ ≈ 9(3.14)$ $ ≈ 28.3 \text{ units}^2$

Now that you’ve read more of our lessons and tips for the Mathematics section of the ASVAB, put your skills to practice with the review quiz below. Try not to reference the above information and treat the questions like a real test.

Part 6 Review Quiz:

ASVAB Free Online Study Guide >>